Covariance
Covariance
Covariance is a non-standardized measure of how much two random variables X and Y change together in a linear way. A strong positive covariance indicates that greater values in one variable correspond to greater values in the other variable. A strong negative covariance indicates that greater values in one variable correspond to smaller values in the other variable.
Requirements:
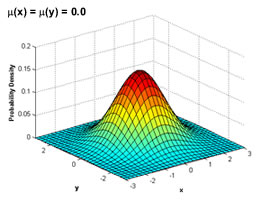
Both random variables must be at least interval scaled and bivariate normal distribution is required.
Illustration of a bivariate normal distribution
Calculation:
Suppose we have two normally distributed random variables x and y.
xi and yi denote the values of x and y for case i.
We then first calculate the cross-product deviation for variables x and y
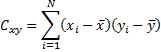
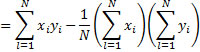
then the covariance is defined as:
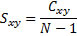
Example of a covariance
A psychologist is interested in his new learning program. 15 Subjects learn a list of 50 words. Learning performance is measured using a recall test. After the first test all subjects are instructed how to use the learning program and then learn a second list of 50 words. Learning performance is again measured with the recall test. In the following table the number of correct remembered words are listed for both tests.
| x | y | x*y | |
| 2 | 1 | 2 | |
| 1 | 2 | 2 | |
| 9 | 6 | 54 | |
| 5 | 4 | 20 | |
| 3 | 2 | 6 | |
| Σ | 20 | 15 | 84 |
We then first calculate the cross-product deviation for variables x and y
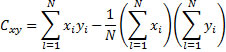
then the covariance is:
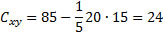
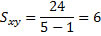
We get a positive covariance, so greater values in x correspond to greater values in y. The following figure illustrates this:
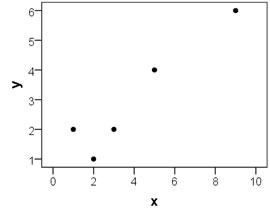
Wiki link
References
Bortz, J. (2005). Statistik für Human- und Sozialwissenschaftler (6th Edition). Heidelberg: Springer Medizin Verlag.























































 Donate IOTA
Donate IOTA