Dependent t-test

Student's t-test for paired samples (dependent)

Comparison of two means from dependent samples.

Examples for dependence:

Repeated measure, parallelized samples, virtual dependence (e.g. twins)

Requirements:

Dependent variable is at least interval scaled and normal distributed.

Hypothesis:

Nondirectional:

H0: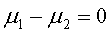    H1:       

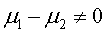
Directional (example):

H0: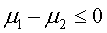      H1: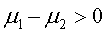

The dependence of two measures from the two samples is gathered from the differences of the measurement pairs.

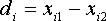
Mean and standard deviation of these differences 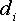are defined as follows:

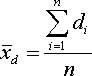
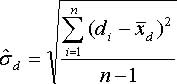
Whereas n is the number of pairs.

The decision between the hypothesis is made according to the sample distribution of .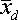

If both populations are normal distributed, the sample distribution is normal, too, with mean

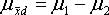
and standard deviation

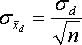
If 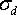is estimated from the sample, we get the following t-distributed equation:

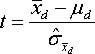
with degree of freedom df = n-1.

Example of a paired samples t-test

A psychologist is interested in his new learning program. 15 Subjects learn a list of 50 words. Learning performance is measured using a recall test. After the first test all subjects are instructed how to use the learning program and then learn a second list of 50 words. Learning performance is again measured with the recall test. In the following table the number of correct remembered words are listed for both tests.

Subject	Score 1	Score 2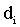
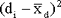1	24	26	-2	0.36
2	17	24	-7	19.36
3	32	31	1	12.96
4	14	17	-3	0.16
5	16	17	-1	2.56
6	22	25	-3	0.16
7	26	25	1	12.96
8	19	24	-5	5.76
9	19	22	-3	0.16
10	22	23	-1	2.56
11	21	26	-5	5.76
12	25	28	-3	0.16
13	16	19	-3	0.16
14	24	23	1	12.96
15	18	22	-4	1.96
Σ			-37	78

n=15

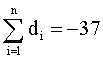
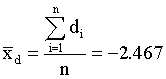
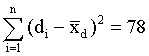
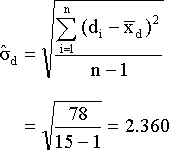
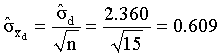
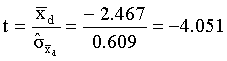
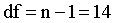
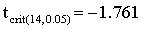
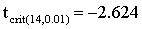
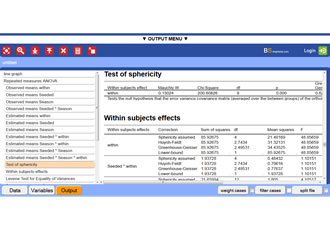
The observed t-value is smaller than the critical t-value (1%, one-tailed). The learning program has a positive effect. Subjects remember more words after the training.


BrightStat output of paired samples t-test example

This is a fictitious example.

How to do this example on BrightStat webapp

Wiki link paired samples t-test