Sign test
Sign test
The sign-test is the alternative test to the Wilcoxon test for dependent data. One requirement of the Wilcoxon test is that the data needs to be at least interval scaled. For the sign test the data needs to be at least ordinal scaled. Comparison of central tendencies of two dependent samples.
Requirements:
Dependent variable must be at least ordinal scaled. Distribition is free.
Idea:
Dependency of the two sample data is considered by taking the differences of paired values. The signs of the individual differences are taken for the test. Under H0 the number of positive differences should approximately equal the number of negative differences. Zero-differences are not considered in the test. The test is a simple binomial test with probability p = 0.5 for a sign to be positive and probability q = 0.5 for a sign to be negative.
Example of a sign test
The effect of a social competence training is tested. 15 Subjects are tested before and after a training for social competence on a seven point scale. Data are ordinal scaled and not normal distributed. The question is, if social competence is enhanced by the training. Raw data are listed in the following table:
| subject | before | after | after - before | sign |
| 1 |
5 |
6 |
1 |
+ |
| 2 |
3 |
2 |
-1 |
- |
| 3 |
4 |
4 |
0 |
|
| 4 |
2 |
4 |
2 |
+ |
| 5 |
1 |
3 |
2 |
+ |
| 6 |
6 |
6 |
0 |
|
| 7 |
7 |
7 |
0 |
|
| 8 |
3 |
5 |
2 |
+ |
| 9 |
2 |
3 |
1 |
+ |
| 10 |
3 |
5 |
2 |
+ |
| 11 |
5 |
5 |
0 |
|
| 12 |
1 |
3 |
2 |
+ |
| 13 |
4 |
4 |
0 |
|
| 14 |
4 |
5 |
1 |
+ |
| 15 |
3 |
2 |
-1 |
- |
Out of the 15 subject, 8 show a positive change, 2 a negative and 5 no change at all. Zero differences are canceled. The analysis is done only with the 8 positive and 2 negative changes. The binomial test tests the probability of k >= 8 positive changes, whereas the probability of a positive change p = 0.5 and the probability of a negative change is q = 0.5.
Hypothesis:
H0: There are less or equal positive as negative changes (p <= 0.5)
H1: There are more positive as negative changes (p > 0.5)
n = 10 (10 subjects are entered in the analysis)
p = 0.5 (probability for positive change under H0 assumption)
q = 1 – p = 0.5 (probability for negative change, under H0 assumption)
The probability for the events k equal or greater 8 is given by:
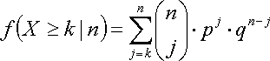
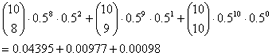
We test only one-sided because the training is expected to produce a positive change. The probability of 8 or more positive changes is 0.0547. Our significance level is 5 percent. The probability is greater than the 5 percent significance level. H1 is discarded. The training does not enhance social compentence.
Remark:
The sign test has little power.
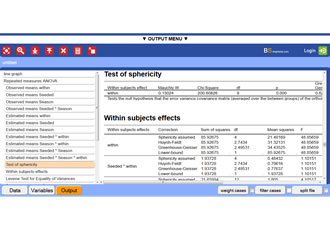
BrightStat output of sign test example
This is a fictitious example.
How to do this example on BrightStat webapp
Wiki link sign test
References
Bortz, J. (2005). Statistik für Human- und Sozialwissenschaftler (6th Edition). Heidelberg: Springer Medizin Verlag.
Conover, W.J. (1999). Practical nonparametric Statistics.(3rd edition). Wiley.























































 Donate IOTA
Donate IOTA